Barisan dan deret Geometri serta deret Geometri tak hingga

BARISAN DAN DERET GEOMETRI


Barisan Geometri

Baris geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan r. Perbandinganatau rasio antara nilai suku dengan nilai suku sebelumnya yang berdekatan selalu sama yaitu r. Sehingga:
\frac{U_n}{U_{(n - 1)}} = r
Sebagai contoh baris 1, 2, 4, 8, 16, merupakan baris geometri dengan nilai
r = \frac{16}{8} = \frac{8}{4} = \frac{4}{2} = \frac{2}{1} = 2
Untuk mengetahui nilai suku ke-n dari suatu barisan geometri dapat diketahui dengan mengetahui nilai suku ke-k dan rasio antar suku yang berdekatan (r). Rumusannya berikut ini:
U_n = U_k \cdot r^{(n - k)}
Jika yang diketahui adalah nilai suku pertama 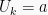 U_k = a dan rasio antar sukunya (r), maka nilai k = 1 dan nilai U_n adalah:
U_n = a \cdot r^{(n - 1)}

Deret Geometri

Deret geometri adalah penjumlahan suku-suku dari suatu barisan geometri. Penjumlahan dari suku suku petama sampai suku ke-n barisan geometri dapat dihitung sebagai:
S_n = U_1 + U_2 + U_3 + \cdots + U_{(n - 1)} + U_n
Atau sebagai:

Barisan Geometri

Baris geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan r. Perbandinganatau rasio antara nilai suku dengan nilai suku sebelumnya yang berdekatan selalu sama yaitu r. Sehingga:
\frac{U_n}{U_{(n - 1)}} = r
Sebagai contoh baris 1, 2, 4, 8, 16, merupakan baris geometri dengan nilai
r = \frac{16}{8} = \frac{8}{4} = \frac{4}{2} = \frac{2}{1} = 2
Untuk mengetahui nilai suku ke-n dari suatu barisan geometri dapat diketahui dengan mengetahui nilai suku ke-k dan rasio antar suku yang berdekatan (r). Rumusannya berikut ini:
U_n = U_k \cdot r^{(n - k)}
Jika yang diketahui adalah nilai suku pertama 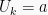 U_k = a dan rasio antar sukunya (r), maka nilai k = 1 dan nilai U_n adalah:
U_n = a \cdot r^{(n - 1)}

Deret Geometri

Deret geometri adalah penjumlahan suku-suku dari suatu barisan geometri. Penjumlahan dari suku suku petama sampai suku ke-n barisan geometri dapat dihitung sebagai:
S_n = U_1 + U_2 + U_3 + \cdots + U_{(n - 1)} + U_n
Atau sebagai:
ar(q+1) = p
Sehingganilai r dapat ditentukan sebagai:
r = \sqrt[q + 1]{\frac{p}{a}}

Deret Geometri Tak hingga

Suatu deret geometri dapat menjumlakan suku-sukunya sampai menuju tak hingga. Apabila deret geometri menuju tak hingga dimana n \rightarrow \infty, maka deret ini dapat dijumlah menjadi:
S_n = U_1 + U_2 + U_3 + U_4 + \cdots
Atau sebagai :
S_n = a + ar + ar^2 + ar^3 + ar^4 + \cdots
Deret geometri tak hingga terdiri dari 2 jenis yaitu konvergen dan divergen. Deret geometri tak hingga bersifat konvergen jika penjumlahan dari suku-sukunya menuju atau mendekati suatu bilangaan tertentu. Sedangkan bersifat divergen jika penjumlahan dari suku-sukunya tidak terbatas. Nilai deret geometri tak hingga dapat diperoleh dengan mengunakan limit. Sebelumnya diketahui bahwa nilai deret geometri  adalah:
S_n = a \frac{(1 - r^n)}{(1 - r)}
Dimana terdapat unsur r^n didalam perhitungannya yang terpengaruh jumlah suku n. Jika n \rightarrow \infty, maka untuk menentukan nilai r^n dapat menggunakan limit yaitu:
lim_{n \rightarrow \infty} r^n
dengan syarat -1 < r < 1.
Dan:
lim_{n \rightarrow \infty} r^n = tak terbatas
dengan syarat r < -1 atau r > 1.
Kemudian hasil limit r^n tersebut dapat dimasukan kedalam perhitungan deret sebagai:
S = a \frac{(1 - lim_{n \rightarrow \infty} r^n)}{(1 -r)} = a \frac{1 - 0}{1 - r} = \infty
dengan syarat -1 < r < 1
Dan:
S = a \frac{(1 - lim_{n \rightarrow \infty} r^n}{(1 - r)} = a \frac{(1 - \infty)}{(1 - r)} = \infty
dengan syarat r < -1 atau r > 1.

Untuk lebih mendalami materi silakan kalian simak video berikut ini 

Setelah kalian mempelajari materi di atas, untuk mengukur kemampuan dalam memahami materi kalian bisa melakukan latihan soal dengan mengunduh soal latihan berikut ini :
>>>>>>>>Latihan soal<<<<<<<<<

Tidak ada komentar:

Posting Komentar

Langganan: Postingan (Atom)